Question

Out of 200 people sampled, 110 had kids. Based on this, construct a 95% confidence interval for the true population proportion of people with kids.

Answer 1

From the sample of n= 200 people,

The proportion of people with kids is:

p'= 110/200= 0.55

The confidence interval for population proportion is given by:

`p' - Z_(\alpha /2) \sqrt[]{(p'(1-p'))/(n) } } \leq P\leq p' + Z_(\alpha /2)\sqrt[]{(p'(1-p'))/(n) } }`

`= p' - Z_(\alpha /2) \sqrt[]{(0.55(0.45))/(200) } } \leq P \le p' + Z_(\alpha /2) \sqrt[]{(0.55(0.45))/(200) } }`

`= p' - Z_(\alpha /2) 0.0352} } } \leq P\le p' + Z_(\alpha /2) 0.0352} }`

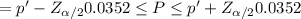
Where P is the population proportion and Z is the critical value at a given level of significance α.