Question

In a school one-third of all 240 students play soccer. Forty four students play both soccer and basketball and sixty students do not play any of these games. How many students play only basketball?

Answer 1

100 students play only basketball.

Explanation:

We are given the following information in the question:

Total number of students in school = 240

Number of students that play soccer =

`(1)/(3)* \text{Total number of students}\\\\=(1)/(3)* 240 = 80`

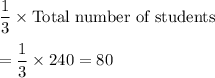
n(S) =80

`n(S\cap B) = 44`

`n(S'\cap B') = 60`

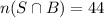
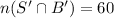
Formula:

`n(S\cup B) = \text{Total} - n(S' \cap B')\\n(S\cup B) = n(S) + n(B) - n(S\cap B)`

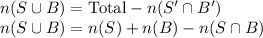
Putting the values, we get,

`n(S\cup B) =240-60=180\\n(S\cup B) = 180 = 80 - 44 + n(B)\\n(B) = 180 - 80 + 44= 144`

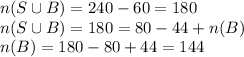
Thus, 144 students play basketball.

Out of these 144, 44 plays soccer as well.

`\text{Student only playing basketball} = 144 -44 = 100`

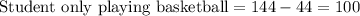
Thus, 100 students play only basketball and not soccer.