Question

write and solve the differential equation that models the following statment. "the rate if change of W with respect to x is proportional to x+18."

Answer 1

`\int k(x + 18)dx = \int kx + 18k dx` =
`k(x^(2) )/(2)` +
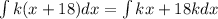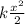`18kx` + C where C is the constant of integration.

Explanation:

i)it is given that the rate of change of W with respect to x is proportional to

x + 18. Therefore
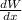`(dW)/(dx)` = k(x + 18) where k is a constant.

ii) Therefore
`\int k(x + 18)dx = \int kx + 18k dx` =
`k(x^(2) )/(2)` +
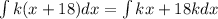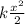`18kx` + C where C is the constant of integration.

iii) the complete solution can only be found if we know the constant of proportion and also the constant of integration.