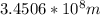Question

A spaceship is on a straight-line path between Earth and its moon. At what distance from Earth is the net gravitational force on the spaceship zero?

Answer 1

To solve this problem we will start from the constants given on the two celestial bodies, that is, the earth and the moon. From there we will seek the balance of forces, where the gravitational force is zero. That distance will remain incognito and will be the one we will seek to find, this is

Given that,

`M_E =5.97*10^24 kg`

`m_m = 7.36*10^22 kg`

`r_E = 6370 km`

`r_m = 1737 km`

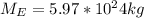
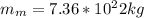
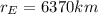
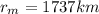
The distance between Earth and Moon

`x = 384403*10^3 m`

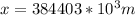
As the net gravitational force is zero we have that

`(GMm')/(d^2) = (Gmm')/((x -d)^2)`

`(M)/(d^2) = (m)/((x -d)^2)`

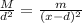
Replacing with our values

`((5.97*10^(24) ))/(d^2) = ((7.36*10^(22)))/((x -d)^2)`

`((x- d)^2)/(d^2)= 0.0123`

`x^2 + d^2 - 2xd = 0.0123 d^2`

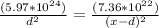
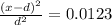
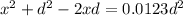
Replacing x as the distance betwen moon and earth,

`(384403 x 10^3)^2+d^2-2(384403 x 10^3)d=0.0123 d^2`

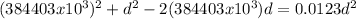
Solving the polynomial we have that

`d =4.3387*10^8 \text{ or } 3.4506*10^(8)`

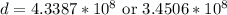
So the minimum value is
`3.4506*10^(8)m`