Question

Find the volume of a regular tetrahedron of side 35cm

Answer 1

Therefore the Volume of a Regular Tetrahedron of side 35 cm is

5028.87 cm³.

Explanation:

Regular Tetrahedron :

A regular tetrahedron is one in which all four faces are equilateral triangles.

There are a total of 6 edges in regular tetrahedron, all of which are equal in length. \

There are four vertices of regular tetrahedron, 3 faces meets at any one vertex.

Given:

Side = edge = a = 35 cm

To Find:

volume of a regular tetrahedron = ?

Solution:

Volume of a Regular Tetrahedron is given as

`\textrm{Volume of a Regular Tetrahedron}=(a^(3))/(6√(2))`

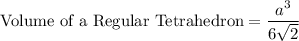
Where, a = edge

Substituting the values we get

`\textrm{Volume of a Regular Tetrahedron}=(35^(3))/(6√(2))=(42875)/(6√(2))=(7145.83)/(√(2))=5052.87\ cm^(3)`

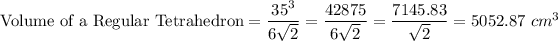
Therefore the Volume of a Regular Tetrahedron of side 35 cm is

5028.87 cm³.