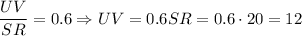Question

In the diagram below, we have $ST = 2TR$ and $PQ = SR = 20$. Find the length $UV$.

Answer 1

12

Explanation:

1.
`ST=2TR` and
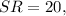`SR=20,` then by segment addition postulate

`ST+TR=SR\\ \\2TR+TR=SR\\ \\3TR=20\\ \\TR=(20)/(3)\\ \\ST=2\cdot (20)/(3)=(40)/(3)`

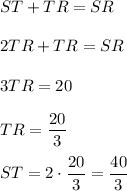
2. Consider triangles PQU and TSU. These triangles are similar by AA similarity theorem (triangles have congruent vertical angles PUQ and TUS and congruent alternate interior angles PQU and TSU). Similar triangles have proportional corresponding sides, so

`(QU)/(US)=(PQ)/(ST)=(20)/((40)/(3))=(60)/(40)=1.5`

`QU=1.5US`

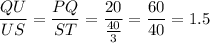
3. Consider triangles QUV and QSR. These triangles are similar by AA similarity theorem. Similar triangles have proportional corresponding sides, so

`(QU)/(QS)=(UV)/(SR)\\ \\(QU)/(QU+US)=(1.5US)/(1.5US+US)=(1.5)/(2.5)=0.6`

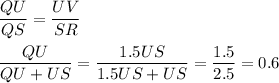
so

`(UV)/(SR)=0.6\Rightarrow UV=0.6SR=0.6\cdot 20=12`