Question

Steve and Elsie are camping in the desert, but have decided to part ways. Steve heads north, at 8 AM, and walks steadily at 2 miles per hour. Elsie sleeps in, and starts walking west at 2.5 miles per hour starting at 10 AM. When will the distance between them be 25 miles?

Answer 1

2.57 hours

Step-by-step explanation:

Let t (hours) be the times it takes for Elsie to walk until they are 25 miles apart. Since Steve is 2 hours earlier, the time it takes for him is t + 2

Distance Steve covers to the North is
`s_s =  2(t + 2)`

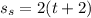
Distance that Elsie covers to the West is
`s_e = 2.5t`

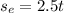
Distance between Steve and Elsie is

`√(s_s^2 + s_e^2) = √((2(t+2))^2 + (2.5t)^2) = 25`

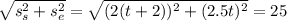
We can solve for t by raise the power on both sides to the 2nd

`(2(t+2))^2 + (2.5t)^2 = 25^2 = 625`

`4(t+2)^2 + 6.25t^2 = 625`

`4(t^2 + 4t + 4) + 6.25t^2 = 625`

`10.25t^2 + 16t - 609 = 0`

`t= (-b \pm √(b^2 - 4ac))/(2a)`

`t= (-16\pm √((16)^2 - 4*(10.25)*(-109)))/(2*(10.25))`

`t= (-16\pm68.74)/(20.5)`

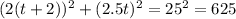
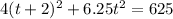
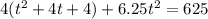
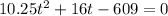
t = 2.57 or t = -4.13

Since t can only be positive we will pick t = 2.57 hours