Question

1 pts
Question 3
ASJX - A
LPX
LXP
XLP
no similar triangles here

Answer 1

Δ SJX ~ Δ LXP

ΔSJX ~ ΔLXP ….{Angle-Angle Similarity Postulate}

Explanation:

Given:

∠XSJ ≅ ∠XLP = 73°

∠SXJ = 54°

∠LXP = 53°

To Prove:

ΔSJX ~ ΔLXP

Proof:

Triangle sum property:

In a Triangle sum of the measures of all the angles of a triangle is 180°.

In ΔLPX,

`\angle L+\angle P+\angle X=180\\\angle P=180-73-53=54\\\angle P=54\°`

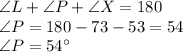
∴ ∠SXJ ≅ ∠LPX = 54° ..........Transitive Property ..( 1 )

In Δ SJX and Δ LXP

∠XSJ ≅ ∠XLP …………..{ measure of each angle is 73° given }

∠SXJ ≅ ∠LPX = 54° ……….....{From ( 1 ) above}

ΔSJX ~ ΔLXP ….{Angle-Angle Similarity Postulate} ..Proved