Question

You can use any coordinate system you like in order to solve a projectile motion problem. To demonstrate the truth of this statement, consider a ball thrown off the top of a building with a velocity vvec at an angle ? with respect to the horizontal. Let the building be 44.0 m tall, the initial horizontal velocity be 8.80 m/s, and the initial vertical velocity be 10.0 m/s. Choose your coordinates such that the positive y-axis is upward, and the positive x-axis is to the right, and the origin is at the point where the ball is released.

(a) With these choices, find the ball's maximum height above the ground, and the time it takes to reach the maximum height.
Maximum height above ground 1 m
Time to reach maximum height 2 s

(b) Repeat your calculations choosing the origin at the base of the building.
Maximum height above ground 3 m
Time to reach maximum height 4 s

Answer 1

a) y₂ = 49.1 m , t = 1.02 s , b) y = 49.1 m , t= 1.02 s

Step-by-step explanation:

a) We will solve this problem with the missile launch kinematic equations, to find the maximum height, at this point the vertical speed is zero

`v_(y)`² =
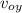`v_(oy)`² - 2 g (y –yo)

The origin of the coordinate system is on the floor and the ball is thrown from a height

y-yo =
=
`v_(oy)` - g t

t =
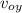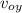`v_(oy)` / g

t = 10 / 9.8

t = 1.02 s

b) the maximum height

y- 44.0 =
`v_(y)`² / 2 g

y - 44.0 = 5.1

y = 5.1 +44.0

y = 49.1 m

The time is the same because it does not depend on the initial height

t = 1.02 s