Question

A major metropolitan newspaper selected a simple random sample of 1,600 readers from their list of 100,000 subscribers.

They asked whether the paper should increase its coverage of local news.

Forty percent of the sample wanted more local news.

What is the 99% confidence interval for the proportion of readers who would like more coverage of local news?

Answer 1

Answer:
`(0.36845,\ 0.43155)`

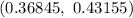
Explanation:

Let p be the population proportion of readers who would like more coverage of local news.

As per given , we have

sample size :=1600

sample proportion :
`\hat{p}=40\%=0.40`

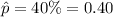
The confidence interval for population proportion is given by :-

`\hat{p}\pm z^* \sqrt{\frac{\hat{p}(1-\hat{p})}{n}}`

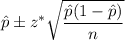
From z-table ,

For 99% confidence interval the z-value is 2.576.

Substitute all the values in the above formula , we get

The 99% confidence interval for the proportion of readers who would like more coverage of local news as

`0.40\pm(2.576) \sqrt{(0.40(1-0.40))/(1600)}`

`0.40\pm(2.576) \sqrt{(0.24)/(1600)}`

`0.40\pm(2.576) √(0.00015)`

`0.40\pm(2.576) (0.0122474487139)`

`0.40\pm0.03155`

`(0.40-0.03155,\ 0.40+0.03155)=(0.36845,\ 0.43155)`

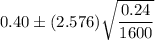
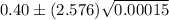
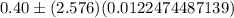
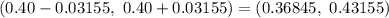
Hence, the 99% confidence interval for the proportion of readers who would like more coverage of local news is
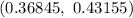`(0.36845,\ 0.43155)` .