Question

Which of the following is a like radical to RootIndex 3 StartRoot 7x EndRoot?

A. 4 (RootIndex 3 StartRoot 7 x EndRoot)
B. StartRoot 7 x EndRoot
C. x (RootIndex 3 StartRoot 7 EndRoot)
D. 7 StartRoot x EndRoot

Answer 1

option a

Explanation:

on edge

Answer 2

A. 4 (RootIndex 3 StartRoot 7 x EndRoot) or
`4(\sqrt[3]{7x})`

Explanation:

Given:

A radical whose value is,
`r_1=\sqrt[3]{7x}`

Now, we need to find the like radical for
`r_1`.

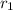Let the like radical be
`r_2`.

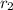As per the definition of like radicals, like radicals are those that can be expressed as multiples of each other.

So, if two radicals
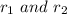`r_1\ and\ r_2` are like radicals, then

`r_1 = n * r_2`

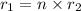
Where, 'n' is a real number.

Here,
`r_1=\sqrt[3]{7x}`

Now, let us check all the options .

Option A:

4 (RootIndex 3 StartRoot 7 x EndRoot) or
`r_2=4\sqrt[3]{7x}`

Now, we observe that
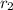`r_2` is a multiple of
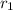`r_1` because

`r_2=4* \sqrt[3]{7x}\\\\ r_2=4* r_1..............(r_1=\sqrt[3]{7x})`

Therefore, option A is correct.

Option B:

StartRoot 7 x EndRoot or
`r_2=√(7x)`

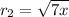
As the above radical is square root and not a cubic root, this option is incorrect.

Option C:

x (RootIndex 3 StartRoot 7 EndRoot) or
`r_2=x\sqrt[3]{7}`

As the term inside the cubic root is not same as that of
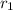`r_1`, this option is also incorrect.

Option D:

7 StartRoot x EndRoot or
`r_2=7√(x)`

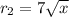
As the above radical is square root and not a cubic root, this option is incorrect.

Therefore, the like radical is option (A) only.