Question

Public opinion in the large city of Bedrock is that 60 percent of the residents are in favor of increasing taxes to fund alternatives to drug addiction treatment and 40 percent are against the increase. What is the approximate probability that more than 150 of the residents surveyed will be against increasing taxes if a random sample of 400 residents are surveyed

Answer 1

Answer: 0.8461

Explanation:

Let p be the proportion of residents are against the increase of taxes to fund alternatives to drug addiction treatment.

As per given , we have p=0.40

A random sample is taken with size : n= 400

Expecting sample proportion :
`\hat{p}=(150)/(400)=0.375`

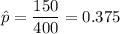
Now , the probability that more than 150 of the residents surveyed will be against increasing taxes if a random sample of 400 residents are surveyed will be :

`P(p>0.375)=P(\frac{\hat{p}-p}{\sqrt{(p(1-p))/(n)}}>\frac{0.375-0.40}{\sqrt{(0.40(0.60))/(400)}})`

`=P(z>\frac{0.375-0.40}{\sqrt{(0.40(0.60))/(400)}})\ \ [\because\ z=\frac{\hat{p}-p}{\sqrt{(p(1-p))/(n)}}]`

`=P(z>-1.02)=P(z<1.02)\ \ [\because \ P(Z>-z)=P(Z<z)]`

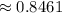`\approx0.8461` [By z-table]

Hence, the approximate probability that more than 150 of the residents surveyed will be against increasing taxes if a random sample of 400 residents are surveyed is 0.8461 .