Question

Ritvik tosses a ball from where he stands on a balcony to his friend on the ground. The

height, in feet, of the ball can be represented by the function d(t) = -16° + 16+ 9,
where represents time in seconds.
Part A: From what height was the ball tossed?
Part B: What is the maximum height of the ball?
Part C: How long does it take the ball to reach its maximum height?

Answer 1

Part A- 9ft

Part B- 13 ft

Part C - 1/2 second

Explanation:

You MUST type in either 0.5 for part C or use the fraction option on the site and do 1/2

Answer 2

Part A: Initial height is 9 feet.

Part B: Maximum height is 13 feet.

Part C: Time taken is 0.5 s.

Explanation:

Given:

The equation to represent the height of the ball is given as:

`d(t)=-16t^2+16t+9`

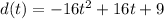
Where, 't' is time passed in seconds.

Part A:

In order to find the initial height of the ball, the initial time must be 0 seconds.

So, plug in 0 for 't' and solve for d(0). This gives,

`d(0)=-16* 0+16* 0+9\\d(0)=9\ ft`

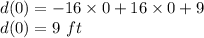
Therefore, the height from which the ball was tossed is 9 feet.

Part B:

The maximum height occurs when the derivative of the given equation with time is 0 as at the relative maximum, the derivative of the function is always 0.

So, differentiating the above equation with respect to time, we get:

`d'(t)=-16(d)/(dt)(t^2)+16(d)/(dt)(t)+(d)/(dt)9`

`d'(t)=-16(2t)+16(1)+0`

`d'(t)=-32t+16`

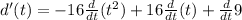
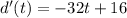
Now, at maximum height, the derivative is 0. So,

`d'(t)=0\\\\-32t+16=0\\\\32t=16\\\\t=(16)/(32)=0.5\ s`

Therefore, the maximum height is obtained by plugging in 0.5 for 't' in the height equation. This gives,

`d(0.5)=-16* 0.5^2+16* 0.5+9\\\\d(0.5)=-4+8+9=13\ ft`

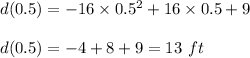
Hence, the maximum height reached by the ball is 13 ft.

Part C:

The time for which the derivative was 0 is the time taken by the ball to reach maximum height.

Therefore, from part B, the time for maximum height is 0.5 s.