Question

The graph shows f(x) = (one-half) Superscript x and its translation, g(x).

On a coordinate plane, 2 exponential functions are shown. f (x) decreases in quadrant 2 and approaches y = 0 in quadrant 1. It goes through (negative 2, 4), (negative 1, 2) and crosses the y-axis at (0, 1). g (x) decreases in quadrant 2 and approaches y = 4 in quadrant 1. It goes through (negative 2, 8), (negative 1, 6) and crosses the y-axis at (0, 5).
Which describes the translation of f(x) to g(x)?

translation of four units up
translation of five units up
translation of four units to the right
translation of five units to the right

Answer 1

a guaranteed

Explanation:

Answer 2

Answer: First option.

Explanation:

Below are shown some transformations for a function
`f(x)`:

1. If
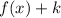`f(x)+k`, the function is translated "k" units up.

2. If
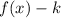`f(x)-k`, the function is translated "k" units down.

3. If
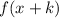`f(x+k)`, the function is translated "k" units to the left.

4. If
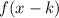`f(x-k)`, the function is translated "k" units to the right.

In this case, you can observe in the graph that the function
`f(x)` intersects the y-axis at:

`y=1`

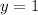
And the function
`g(x)` intersects the y-axis at:

`y=5`

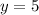
Knowing this, you can idenfity that:

`g(x)=f(x)+4`

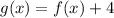
Therefore, you can conclude that the statement that best describes the translation of
`f(x)` to
`g(x)` is: "Translation of four units up".