Question

How many liters of 0.615 M NaOH will be needed to raise the pH of 0.385 L of 5.13 M sulfurous acid (H2SO3) to a pH of 6.247?

Answer 1

Volume of NaOH required = 3.61 L

Step-by-step explanation:

H2SO3 is a diprotic acid i.e. it will have two dissociation constants given as follows:

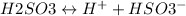`H2SO3\leftrightarrow H^(+)+HSO3^(-)` --------(1)

where, Ka1 = 1.5 x 10–2 or pKa1 = 1.824

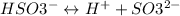`HSO3^(-)\leftrightarrow H^(+)+SO3^(2-)` --------(2)

where, Ka2 = 1.0 x 10–7 or pKa2 = 7.000

The required pH = 6.247 which is beyond the first equivalence point but within the second equivalence point.

Step 1:

Based on equation(1), at the first eq point:

moles of H2SO3 = moles of NaOH

`i.e. \ 5.13\  moles/L*0.385L = moles\  NaOH\\therefore, \ moles\  NaOH = 1.98\ moles\\V(NaOH)\ required = (1.98\ moles)/(0.615\ moles/L) =3.22L`

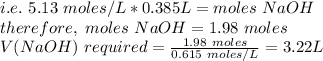
Step 2:

For the second equivalence point setup an ICE table:

`HSO3^(-)+OH^(-)\leftrightarrow H2O+SO3^(2-)`

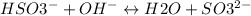
Initial 1.98 ? 0

Change -x -x x

Equil 1.98-x ?-x x

Here, ?-x =0 i.e. amount of OH- = x

Based on the Henderson buffer equation:

`pH = pKa2 + log([SO3]^(2-) )/([HSO3]^(-) ) \\6.247 = 7.00 + log(x)/((1.98-x)) \\x=0.634 moles`

Volume of NaOH required is:

`(0.634\ moles)/(0.615 moles/L)=0.389L`

Step 3:

Total volume of NaOH required = 3.22+0.389 =3.61 L