Answer:

Explanation:
We are given:
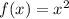
![interval = [a,b] = [0,2]](https://img.qammunity.org/2021/formulas/mathematics/college/fdyxq7c1vktbv9srtjejchioy3y6103w79.png)
Since
 ⇒
⇒
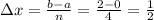
Riemann sum is area under the function given. And it is asked to find Riemann sum for the left endpoint.
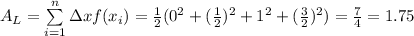
Note:
If it will be asked to find right endpoint too,
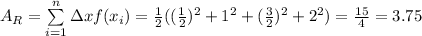
The average of left and right endpoint Riemann sums will give approximate result of the area under
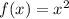 and it can be compared with the result of integral of the same function in the interval given.
and it can be compared with the result of integral of the same function in the interval given.
So,
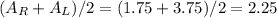
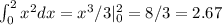
Result are close but not same, since one is approximate and one is exact; however, by increasing sample rates (subintervals), closer result to the exact value can be found.