Question

The dollar value of two investments after t years is given by f(t) =1800(1.055)t and g(t) = 9500(1.041)t. Solve the equation f(t) = g(t). What does your solution tell you about the investments?

Answer 1

The solution tells me that in 124.5 years the value of the dollar in both investments will be the same

Explanation:

Let

t ----> the number of years

f(t) ---> the dollar value of one investment

g(t) ---> the dollar value of the other investment

we have

`f(t)=1,800(1.055)^t`

`g(t)=9,500(1.041)^t`

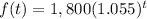
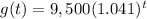
Solve the equation f(t)=g(t)

`9,500(1.041)^t=1,800(1.055)^t`

`(9,500)/(1,800)=((1.055)^t)/((1.041)^t)`

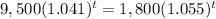
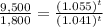
Rewrite

`(9,500)/(1,800)=((1.055)/(1.041))^t`

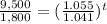
Apply log both sides

`log((9,500)/(1,800))=log((1.055)/(1.041))^t`

`log((9,500)/(1,800))=tlog((1.055)/(1.041))`

`t=log((9,500)/(1,800))/log((1.055)/(1.041))`

`t=124.5\ years`

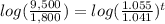
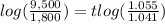
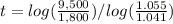
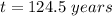
therefore

The solution tells me that in 124.5 years the value of the dollar in both investments will be the same