Question

Find the average value of the function on the given interval.
f(x)=√x+1; [3,8]

Answer 1

3.3242

Explanation:

Given function in the question:

f(x) = √x + 1 ; [3 , 8]

Now,

The average value is calculated as:

⇒
`(1)/(b-a)\int\limits^b_a {f(x)} \, dx`

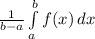
Therefore,

for the given data

a = 3

b = 8

f(x) = √x + 1

Thus,

average =
`(1)/(8-3)\int\limits^(8)_3 {√(x)+1} \, dx`

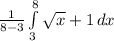
or

average =
`(1)/(8-3)*[ \frac{x^{(1)/(2)+1}}{(1)/(2)+1}+x]^(8)_3`

or

average =
`(1)/(8-3)*[\frac{x^{(3)/(2)}}{(3)/(2)}+x]^(8)_3`

or

Average =
`(1)/(5)*[ (\frac{8^{(3)/(2)}}{(3)/(2)}+8)-(\frac{3^{(3)/(2)}}{(3)/(2)}+3)]`

or

Average =
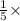`(1)/(5)*` [23.085 - 6.464 ]

or

Average = 3.3242