Question

Pumping alone at respective constant one inlet pipe fills an empty tank to 1/2 of capacity in 3 hours and a second inlet pipe fills the same empty tank to 2/3 of capacity in 6 hours.

How many hours will it take both pipes, pumping simultaneously at their respective constant rates, to fill the empty tank to capacity?
A. 3.25
B. 3.6
C. 4.2
D. 4.4
E. 5.5

Answer 1

Answer: B. 3.6

Explanation:

Given : Time taken by one inlet pipe to empty
`(1)/(2)` of tank = 3 hours

⇒ Time taken by one inlet pipe to empty tank (entire) = 2 x 3 hours

= 6 hours →
`t_1`

Time taken by second inlet pipe to empty
`(2)/(3)` of tank = 6 hours

⇒ Time taken by second inlet pipe to empty tank (entire) =
`(3)/(2)*6= 3*6`

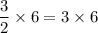
= 9 hours →
`t_2`

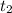
If both pipes are pumping simultaneously at their respective constant rates to fill the empty tank to capacity.

Then time taken by them to fill the empty tank to capacity would be
`(t_1t_2)/(t_1+t_2)`

`=((6)(9))/(6+9)=(54)/(15)=(18)/(5)=3.6`

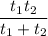
Hence, it will take 3.6 hours to fill the empty tank to capacity .

Therefore , the correct answer is B. 3.6 .