Question

Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disaproves the statement.

The dot product of parallel vectors is zero,

Answer 1

False

Explanation:

the dot product between two vectors A and B is:

A·B=AB
`cos\theta`

where
`\theta` is the angle between the vectors, if they are parallel, this angle is zero. so
`\theta=0`

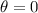
and so the dot product is:

A·B =AB
`cos(0)`

and since
`cos (0)=1`

the dot product is equal to

A·B=AB

The dot product of parallel vectors is NOT zero