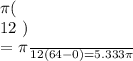Question

Find the volume of the solid of revolution formed by rotating the bounded region about the x-axis.

f(x)=x^2/4, y=0, x=4.

Answer 1

5.333 \pi

Explanation:

Given is a function exponential as

`f(x) = (x^2)/(4)`

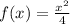
The region bounded by the above curve, y =0 , x=4 is rotated about x axis.

The intersection of curve with x axis is at x=0

The limits for x are 0 and 4

The volume when rotated through x axis is found by

`\pi\int\limits^b_a {f(x)^2} \, dx`

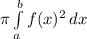
Here a = 0 and b =4

volume =
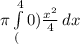
`\pi\int\limits^4_(0) (x^2)/(4) \, dx`

=
`\pi (\frac{x^3} }{12} )\\= (\pi)/(12) (64-0)\\= 5.333 \pi`