Question

Determine whether the statement is true or false, and explain why.

Integration by parts should be used to evaluate ∫^1_0 x^2/x^3+1 dx.

Answer 1

False

Explanation:

In this case, i woudnt reccomend to use integration by parts, becuase you are not simplifying the expression by doing an integration and a derivation. It is not easy to integrate 1/x³+1, and if you derivate it, then a natural logarithm would appear, and the integral wont be easier after this parts step.

It is a better idea to use integration by substitution. Note that if you replace x³+1 by a variable y, we have that dy = 3x² dx. We can easily make a 3xdx appear in the integral by multiplying and dividing by 3, solving the integral easily:

`\int\limits_0^1 x^2/x^3+1 \, dx = 1/3 * \int\limits_1^2 du/u = (ln(2) - ln(1) )/3`

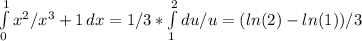
(Note that, if x ranges from 0 to 1, then u = x³+1 ranges from 0³+1 = 1 to 1³+1 = 2)