Question

A rancher decides to make 4 identical and adjacent rectangular pens against her barn each with an area of 100m^2. What are the dimensions of each pen that minimize the amount of fence that must be used?

Answer 1

Dimensions of each pen are
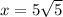`x=5√(5)` and
`y=4√(5)`.

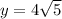Explanation:

Please find the attachment.

We have been given that a rancher decides to make 4 identical and adjacent rectangular pens against her barn each with an area of
`100m^2`.

The area of rectangle is width times length, so we can set an equation as:

`x\cdot y=100...(1)`

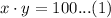
The fence of 4 identical and adjacent rectangular pens will be equal to perimeter of 4 adjacent rectangles as:

`\text{Perimeter}=4x+5y`

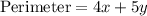
From equation (1), we will get:

`y=(100)/(x)`

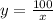
Upon substituting this value in perimeter equation, we will get:

`P=4x+5((100)/(x))`

`P=4x+(500)/(x)`

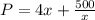
Now, we will find the first derivative of perimeter equation as:

`P=4x+500x^(-1)`

`P'=4-500x^(-2)`

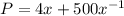
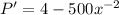
Now, we will equate 1st derivative equal to 0 to find the critical points:

`4-500x^(-2)=0`

`-(500)/(x^(2))=-8`

`(500)/(x^(2))=4`

`4x^(2)=500`

`x^(2)=125`

`x=√(125)`

`x=5√(5)`

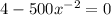
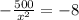
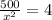
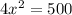
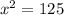
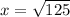
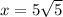
Now, we will find 2nd derivative of above equation as:

`P''=0-(-2*500)x^(-2-1)`

`P''=1000x^(-3)`

`P''=(1000)/(x^3)`

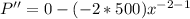
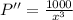
Now, we will check point
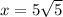`x=5√(5)` in 2nd derivative, if it is positive, then x will be a minimum point.

`P''(5√(5))=(1000)/((5√(5))^3)`

`P''(5√(5))=(1000)/(625√(5))`

`P''(5√(5))=0.71554`

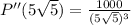
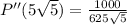
Since 2nd derivative is positive, so fence will be minimum at
`x=5√(5)`.

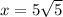Now, we will substitute
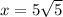`x=5√(5)` in equation
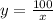`y=(100)/(x)` to solve for y as:

`y=(100)/(5√(5))`

`y=(20)/(√(5))`

`y=4√(5)`

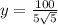
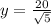
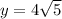
Therefore, the fence will be minimum at
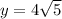`y=4√(5)`.