Question

Solve 6g hahahahshhshhshhshs

Answer 1

6g) We proved the equality
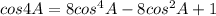`cos4A=8cos^(4)A-8cos^(2)A+1` is true and hence proved.

Explanation:

Given equation is
`cos4A=8cos^(4)A-8cos^(2)A+1`

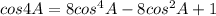
To prove the equality LHS=RHS

`cos4A=8cos^(4)A-8cos^(2)A+1`

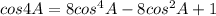
Let us take LHS

`cos4A=cos2(2A)`

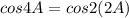
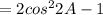`=2cos^(2)2A-1` (since using
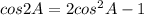`cos2A=2cos^(2)A-1` here A=2A)

`=2[(2cos^(2)2A-1)^2]-1`

`=2[2^2cos^(4)2A-2* 2cos^(2)2A+1]-1` (using the formula
`(a-b)^2=a^2-2ab+b^2` here
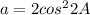`a=2cos^(2)2A` and b=1)

`=2[4cos^(4)2A-4cos^(2)2A+1]-1`

`=8cos^(4)2A-8cos^(2)2A+2-1`

`=8cos^(4)2A-8cos^(2)2A+1`

`=8cos^(4)2A-8cos^(2)2A+1=RHS`

`cos4A=8cos^(4)2A-8cos^(2)2A+1=RHS`

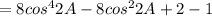
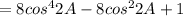
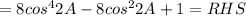
Therefore LHS=RHS.

We proved the equality
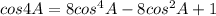`cos4A=8cos^(4)A-8cos^(2)A+1` is true and hence proved.