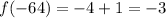Answer:
Part 1)
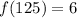
Part 2)
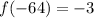
Explanation:
we have
![f(x)=\sqrt[3]{x} +1](https://img.qammunity.org/2021/formulas/mathematics/middle-school/d4mwiltj5u9gdkj9qn2bsrv7o8e3nnjl67.png)
Part 1) Find f(125)
we know that
f(125) is the value of the function f(x) when the value of x is equal to 125
so
For x=125
substitute in the function
![f(125)=\sqrt[3]{125} +1](https://img.qammunity.org/2021/formulas/mathematics/middle-school/9n9e79zl4g0kjvl8lg215bveu4v4bna02t.png)
Remember that
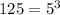
substitute
![f(125)=\sqrt[3]{5^(3)} +1](https://img.qammunity.org/2021/formulas/mathematics/middle-school/g3dujcutsejbqclp6vlkm0urydwj3hbdpj.png)
Applying the power of rule
![\sqrt[3]{5^(3)}=(5^(3))^{(1)/(3)}= (5)^{3*(1)/(3)}=5](https://img.qammunity.org/2021/formulas/mathematics/middle-school/ddx5k3sw8kgkx7uuln78ftobg1cxv4tge6.png)
substitute
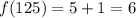
Part 2) Find f(-64)
we know that
f(-64) is the value of the function f(x) when the value of x is equal to -64
so
For x=-64
substitute in the function
![f(-64)=\sqrt[3]{-64} +1](https://img.qammunity.org/2021/formulas/mathematics/middle-school/lasq38ys5q5pub0vae11gqie2js13redi8.png)
Remember that
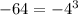
substitute
![f(-64)=\sqrt[3]{-4^(3)} +1](https://img.qammunity.org/2021/formulas/mathematics/middle-school/v15zgs5l0w2bxjhgmhbdx35lp065r5j5t0.png)
Applying the power of rule
![\sqrt[3]{-4^(3)}=(-4^(3))^{(1)/(3)}= (-4)^{3*(1)/(3)}=-4](https://img.qammunity.org/2021/formulas/mathematics/middle-school/f8ca0glrszgh8c8ge2zbhoe3amb2k8mt85.png)
substitute