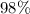Answer:
The probability of missing both free-throw shots = 2%
The probability of making at least 1 free-throw shot = 98%
Explanation:
Given :
Probability that she misses the first shot = 40%
Probability she misses the second shot = 5%
Solution:
Part A: The probability of missing both free-throw shots:
The two shots are independent events so, we can use rule of independent events
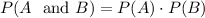
=>
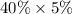
=>

=>
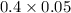
=>
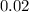
=>
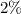
Part B: The probability of making at least 1 free-throw shot
Probability of making at least 1 free throw show shot = 1 - probability of miss both the shots
=>
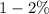
=>
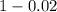
=>
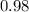
=>