Question

The marks on a statistics test are normally distributed with a mean of 62 and a variance of 225. If the instructor wishes to assign Bs or higher to the top 25% of the students in the class, what mark is required to get a B or higher?

Answer 1

79 marks are required to get a B or higher.

Explanation:

We have been given that the marks on a statistics test are normally distributed with a mean of 62 and a variance of 225. The instructor wishes to assign Bs or higher to the top 25% of the students in the class.

We will use normal distribution table and z-score formula to solve our given problem.

`z=(x-\mu)/(\sigma)`, where,

z= Z-score,

x = Sample score,

`\mu=\text{Mean}\\\sigma=\text{Standard deviation}`

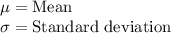
We know that standard deviation is equal to square-root of variance, so SD for given data would be
`√(225)=15`.

`z=(x-62)/(25)`

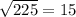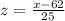
We know that top 25% means 75% and more.

Let us find z-score corresponding to 75% or 0.75 using normal distribution table.

`0.68=(x-62)/(25)`

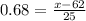
Let us solve for x.

`0.68*25=(x-62)/(25)*25`

`17=x-62`

`17+62=x-62+62`

`79=x`

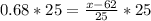
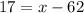
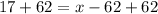
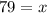
Therefore, 79 marks are required to get a B or higher.