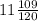Answer:
 or
or
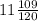
Explanation:
Given:
A farmer has a basket of peaches. He gives ⅓ of the peaches to one person, ¼ to another, ⅕ to another, ⅛ to another, and then gives 7 peaches to a 5th person.
Remaining peaches = 4
We need to find the original number of peaches in the basket.
The farmer gives the total number of peaches =
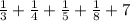
Let x be the former gives the total number of peaches
We multiply and divide by 120 in right side of the above equation because of 120 is divided by all given denominator and then simplify.
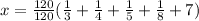
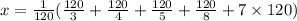
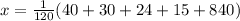

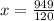
We add the remaining peaches by given peaches for the original number of peaches in the basket.
Original number of peaches =

Original number of peaches =

Original number of peaches =
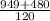
Original number of peaches =

Original number of peaches =
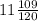
Therefore the original number of peaches in the basket is
 or
or