Answer:
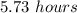 or
or
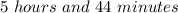
Explanation:
You can use the following work-rate formula:
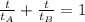
In this case let be
 the time it takes for Natalie to pick 40 bushels,
the time it takes for Natalie to pick 40 bushels,
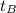 the time it takes for Mary to pick 40 bushels and
the time it takes for Mary to pick 40 bushels and
 the time it takes to pick 40 bushels if they work together.
the time it takes to pick 40 bushels if they work together.
Based on the information given in the exercise, you can identify that:
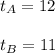
Then, knowing this values, you need to substitute them into the formula:
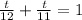
Finally, you must solve for "t" in order to find its value.
The result is:

Since
 :
:
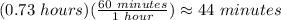
Therefore it would take 5 hours and 44 minutes to pick 40 bushels if they worked together.