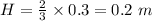Question

A hollow cubical box is 0.30 m on an edge. This box is floating in a lake with one-third of its height beneath the surface. The walls of the box have a negligible thickness. Water is poured into the box. What is the depth of the water in the box at the instant the box begins to sink?

Answer 1

Step-by-step explanation:

Given

length of cubical box
`h=0.3 m`

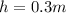
If density of object
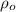`\rho _o` and density of lake liquid
`\rho _l`

when it is in equilibrium one-third of its height

Buoyancy force will be equal to weight of cubical box

`\rho * h^3* g=\rho _l* h^2* (h)/(3)* g`

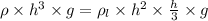
therefore
`(\rho _o)/(\rho _w)=(1)/(3)`

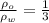
When water start Pouring in it then height of liquid at which box started to sink

Let H be that height

`\rho * h^3* g+\rho * h^2* H* g=\rho _l* h^2* h* g`

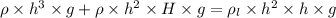
cancel out the common terms and divide by density of lake

`(\rho _o)/(\rho _l)* h+H=h`

`H=h-(h)/(3)=(2)/(3)h`

`H=(2)/(3)* 0.3=0.2\ m`