Question

Let T: Mmxn(R)Mmxn(R) be the function defined

byT(A)=AT ( the transpoose of A) for A
inMmxn(R). Is T a linear transformation? Justify your
answer.

Answer 1

True. See the explanation and proof below.

Explanation:

For this case we need to remeber the definition of linear transformation.

Let A and B be vector spaces with same scalars. A map defined as T: A >B is called a linear transformation from A to B if satisfy these two conditions:

1) T(x+y) = T(x) + T(y)

2) T(cv) = cT(v)

For all vectors
`x,y \in V` and for all scalars
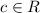`c \in R`. And A is called the domain and B the codomain of T.

Proof

For this case the tranformation proposed is t:
`M_(mxn) (R) > M_(nxm) (R)`

Where
`T(A) = A^T`

For this case we have the following assumption:

1) The transpose of an nxm matrix is an nxm matrix

And the following conditions:

2)
`T(A+B) = (A+B)^T = A^T + B^T = T(A) + T(B)`

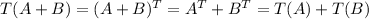
And we can express like this
`T(A+B) =T(A) + T(B)`

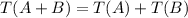
3) If
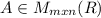`A \in M_(mxn)(R)` and
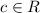`c \in R` then we have this:

`T(cA) = (cA)^T = cA^T = cT(A)`

And since we have all the conditions satisfied, we can conclude that T is a linear transformation on this case.