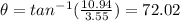Question

A motorboat travels across a lake at a speed of 10 mph at a bearing of 25°. The current of the lake due to the wind

is a steady 2 mph at a bearing of 340°.
a. Draw a diagram that shows the two velocities that are affecting the boat’s motion across the lake.
b. What is the resulting speed and direction of the boat?

Answer 1

a) Figure attached

b)
`v_r = √(3.55^2 +10.94^2)=11.50 mph`

`\theta = tan^(-1) ((10.94)/(3.55))=72.02`

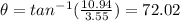
Explanation:

Part a

See the figure attached.

Part b

For this case first we need to find the vectors of velocity for the boat and the wind like this:

`b= <10 cos(65), 10 sin(65)>= <4.23, 9.06> mph`

`w= <2 cos(110), 2 sin(110)>= <-0.68, 1.88> mph`

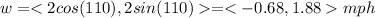
And now if we want to find the resulting velocity we just need to add the vector:

`b + w = <4.23-0.68, 9.06+1.88>=<3.55, 10.94>mph`

And the resultant magnitude would be:

`v_r = √(3.55^2 +10.94^2)=11.50 mph`

And if we want the resultant angle we can do this:

`\theta = tan^(-1) ((10.94)/(3.55))=72.02`