Answer:
$4500
Explanation:
The amount a has is 1/3 total of b, c, and d
 eq. 1
eq. 1
The amount b has is 1/4 total of a, c, and d
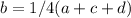 eq. 2
eq. 2
The amount c has is 1/5 total of a, b, and d
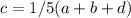 eq. 3
eq. 3

substitute the value of
 in above equations
in above equations
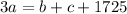
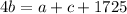
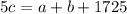
Rearrange the equations to form matrices


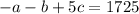
![X=\left[\begin{array}{c}a&b&c\\\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/e175ew51hxapl3o4p1rrxqbtn3crlues4c.png)
![A=\left[\begin{array}{ccc}3&-1&-1\\-1&4&-1\\-1&-1&5\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/ji1ths4c2fvigxufw566i5uf298ubxvvik.png)
![B=\left[\begin{array}{c}1725&1725&1725\\\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/r6ajay7oh7v75p6nnutvlhh35kmf6msp94.png)
As we know
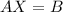
To find the values of matrix X, we take inverse of matrix A and multiply it with matrix B
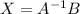
![\left[\begin{array}{c}a&b&c\\\end{array}\right]=\left[\begin{array}{ccc}3&-1&-1\\-1&4&-1\\-1&-1&5\end{array}\right]^(-1) \left[\begin{array}{c}1725&1725&1725\\\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/nt92tukaxyfofnsg4an9pdgc77bo2acaf2.png)
Solving using calculator yield the following results
![X=\left[\begin{array}{c}1125&900&750\\\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/d4tk5er5dztzucjpxzf12u7dwk91fywv9n.png)
so,
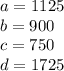
Finally, altogether they have

Verification:
Lets verify if have got the right answer!
Substitute the amount of b, c, and d in eq. 1


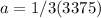
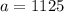 (proved)
(proved)
Substitute the amount of a, c, and d in eq. 2
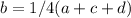

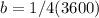
 (proved)
(proved)
Substitute the amount of a, b, and d in eq. 3
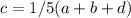


 (proved)
(proved)