Question

Given a = 54, b = 68, and c = 90, use the law of cosines

tofind the angleof the oblique triangle (not a righttriangle). Round to
the nearest whole number.

Answer 1

94°

Explanation:

Oblique triangles are of two types: acute or obtuse triangle. They are not right triangles since they have no right angle.

This question can be answer using the Law of cosines, which states that:

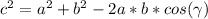`\\ c^2 = a^2 + b^2 - 2a*b * cos(\gamma)` [1]

Where
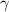`\\ \gamma` is the angle of the respective opposite side c, a and b are the other triangles' sides.

Well, since we have all the information needed to find
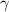`\\ \gamma`, that is, a = 54, b = 68 and c = 90, we calculate it using the formula [1] as follows:

`\\ 90^2 = 54^2 + 68^2 - 2*(54)*(68)*cos(\gamma)`

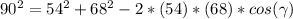
Solving this equation for
`\\ cos(\gamma)`:

`\\ 90^2 - 54^2 - 68^2 = - 2*(54)*(68)*cos(\gamma)`

`\\ 8100 - 2916 - 4624 = - 7344*cos(\gamma)`

`\\ 560 = - 7344*cos(\gamma)`

`\\ (560)/(-7344) = cos(\gamma)`

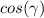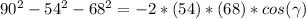
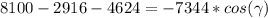
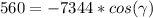
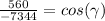
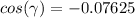`\\ cos(\gamma) = - 0.07625` (for four significant figures)

To obtain
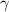`\\ \gamma`, we need to determine which angle has a
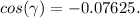`\\ cos(\gamma) = -0.07625.` For this, it is necessary the
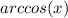`\\ arccos(x)` function, also expressed as
`\\ cos^(-1)(x).`

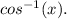
Then

`\\ cos^(-1)[cos(\gamma)] = cos^(-1)(-0.07625)`

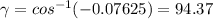`\\ \gamma = cos^(-1)(-0.07625) = 94.37` degrees.

Rounding the result to the nearest whole number, the answer is
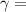`\\ \gamma =` 94°.

The rest of the angles can be obtained using the Law of sines.