Question

For Exercises 6–9, determine the number of real solutions for each quadratic equation without solving.

6. p^2 + 7p + 33 = 8 − 3p
7. 7x^2 + 2x + 5 = 0
8. 2y^2 + 10y = y^2 + 4y − 3
9. 4z^2 + 9 = −4z

Answer 1

1) one real solution

2) no real solution

3) two real solutions

4) no real solution

Explanation:

We have to determine the number of real solutions for each quadratic equation without solving.

`ax^2 + bx +c=0\\D = b^2-4ac\\\text{If D is positive there are two real solutions}\\\text{Pif D is zero then there is one real solution}\\\text{if D is negative then there are no real solution.}`

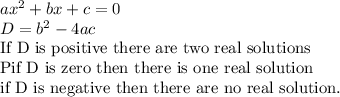
1)

`p^2 + 7p + 33 = 8 - 3p\\p^2+10p+25=0\\D = 10^2 - 4(1)(25) = 0`

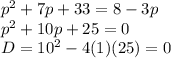
Thus, the quadratic equation has one real solution.

2)

`7x^2 + 2x + 5 = 0\\D = 2^2 - 4(7)(5) < 0`

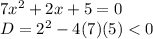
Thus, the quadratic equation has no real solution.

3)

`2y^2 + 10y = y^2 + 4y - 3\\y^2+6y+3=0\\D = 6^2 - 4(1)(3) > 0`

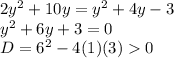
Thus, the quadratic equation has two real solutions.

4)

`4z^2 + 9 = -4z\\4z^2 + 4z + 9 = 0\\D =4^2 - 4(4)(9) < 0`

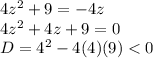
Thus, the quadratic equation has no real solution.