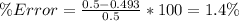Question

Your teacher will report the mean and standard deviation of the sampling distribution created by the class.

8. How does the mean of the sampling distribution compare with the population proportion of 0.50?

Answer 1

`\hat p = (\sum_(i=1)^(40) \hat p_i)/(40)`

`\hat p = 0.493`

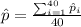
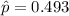
And the deviation is given by this formula:

`s_(\hat p)= (\sum_(i=1)^(40) (\hat p_i - \hat p)^2)/(n-1)= 0.085`

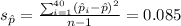
And as we can see the population proportion expected for the number of heads 0.5 is very close to the mean of the sampling distribution, the error is :

`\% Error = (0.5-0.493)/(0.5)* 100 = 1.4\%`

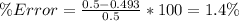
Explanation:

Assuming the data on the figure attached. We ar assuming that this is a sampling distribution of sample proportions of heads in 40 flips of a coin.

As we can see we have the following values:

0.25, 0.35, 0.375,0.375, 0.40,0.40,0.40, 0.425,0.425,0.425, 0.45,0.45,0.45,0.45, 0.475,0.475,0.475, 0.475,0.475, 0.50,0.50,0.50, 0.525,0.525,0.525,0.525, 0.55,0.55,0.55,0.55,0.55, 0.575,0.575,0.575 0.575, 0.575, 0.60,0.60, 0.65,0.65

And we can calculate the sample proportion with the following formula:

`\hat p = (\sum_(i=1)^(40) \hat p_i)/(40)`

`\hat p = 0.493`

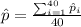
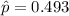
And the deviation is given by this formula:

`s_(\hat p)= (\sum_(i=1)^(40) (\hat p_i - \hat p)^2)/(n-1)= 0.085`

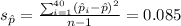
And as we can see the population proportion expected for the number of heads 0.5 is very close to the mean of the sampling distribution, the error is :

`\% Error = (0.5-0.493)/(0.5)* 100 = 1.4\%`