Question

Betting odds are usually stated against the event happening (against winning). The odds against event W are the ratio P(not W) P(W) = P(Wc) P(W) . In horse racing, the betting odds are based on the probability that the horse does not win.

(a) Show that if we are given the odds against an event W as a:b, the probability of not W is given by P(Wc) = a a + b . P(W) = − P(not W) P(not W) P(W) = a P(not W) − P(not W) = a b[P(not W)] = [1 − P(not W)] b[P(not W)] + a[P(not W)] = (a + b)[P(not W)] = P(not W) = a +
(b) In a recent Kentucky Derby, the betting odds for the favorite horse were 8 to 5. Use these odds to compute the probability that the favorite horse would lose the race. What is the probability that the favorite horse would win the race? (Round your answers to two decimal places.) P(lose) = P(win) =
(c) In the same race, the betting odds for a second horse were 5 to 1. Use these odds to estimate the probability that this horse would lose the race. What is the probability that this horse would win the race? (Round your answers to two decimal places.) P(lose) = P(win) =
(d) One of the horses was a long shot, with betting odds of 26 to 1. Use these odds to estimate the probability that the long shot would lose the race. What is the probability the horse would win the race? (Round your answers to two decimal places.) P(lose) = P(win) =

Answer 1

a) it has been shown

b) P(lose) = 0.62, P(win) = 0.38

c) P(lose) = 0.83, P(win) = 0.17

d) P(lose) = 0.96, P(win) = 0.04

Explanation:

a) Since
`(a)/(b) =(P(W_c))/(1-P(W_c))`

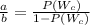
Then by cross-multiplication,

`a(1-P(W_c))=bP(W_c)\\a-aP(W_c)=bP(W_c)\\a=bP(W_c)+aP(W_c)=(a+b)P(W_c)`

So,
`P(W_c)=(a)/(a+b)`

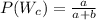
b) P(lose) = 8/(8+5) = 8/13 = 0.62

P(win) = 5/(8+5) = 5/13 = 0.38

c) P(lose) = 5/(5+1) = 5/6 = 0.83

P(win) = 1/(5+1) = 1/6 = 0.17

d) P(lose) = 26/(26+1) = 26/27 = 0.96

P(win) = 1/(26+1) = 1/27 = 0.04