Question

Can the positive integer p be expressed as the product of two integers, each of which is greater than 1? 1. 31 < p < 37 2. p is odd.

Answer 1

1)
`31 < p<37`

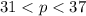
For this case the values that satisfy the inequality are: 32,33,34,35,36

And we can analyze one by one the number:

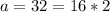`a=32= 16*2` so then is a composite number because 2>1 and 16>1

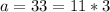`a=33= 11*3` so then is a composite number because 3>1 and 11>1

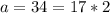`a=34= 17*2` so then is a composite number because 2>1 and 17>1

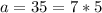`a=35= 7*5` so then is a composite number because 7>1 and 5>1

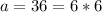`a=36= 6*6` so then is a composite number because 6>1 and 6>1

So then part 1 is correct and we can see that the statement is enough or sufficient all the values on 31<P<37 are composite numbers.

2) For this cas this statement is FALSE, since we have a counterexample on this case:

`a=3=1*3` and 3 is not a composite number since 1 is not >1

And since we have one element that not satisfy the condition that's FALSE.

Explanation:

For this question we need to use the following definition "If an integer p can b expressed as the product of two integers, each of which that is greater then 1, then the integer p can be considered as a composite number". And this number is not the same as prime number.

Part 1

`31 < p<37`

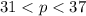
For this case the values that satisfy the inequality are: 32,33,34,35,36

And we can analyze one by one the number:

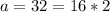`a=32= 16*2` so then is a composite number because 2>1 and 16>1

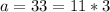`a=33= 11*3` so then is a composite number because 3>1 and 11>1

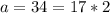`a=34= 17*2` so then is a composite number because 2>1 and 17>1

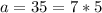`a=35= 7*5` so then is a composite number because 7>1 and 5>1

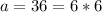`a=36= 6*6` so then is a composite number because 6>1 and 6>1

So then part 1 is correct and we can see that the statement is enough or sufficient all the values on 31<P<37 are composite numbers.

Part 2

For this cas this statement is FALSE, since we have a counterexample on this case:

`a=3=1*3` and 3 is not a composite number since 1 is not >1

And since we have one element that not satisfy the condition that's FALSE.