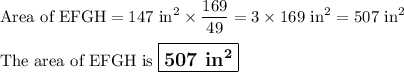Question

Quadrilateral ABCD is similar to Quadrilateral EFGH. Diagonal AC has length 7 and diagonal EG has length 13. What is the scale factor that describes a dilation from BC to FG? Give the exact scale factor and state whether the dilation is an expansion or a contraction.

If side AB has length 17/26 what is the length of side EF? Give the exact, un-rounded value.




PLEASE HELP ASAP

If the area of ABCD is 147 square inches, what is the area of EFGH? Give the exact answer.

Answer 1

`\large \boxed{\text{A. }(13)/(7)\text{; B. }(17)/(14) \text{; C. 507 in}^(2)}`

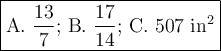
Explanation:

A. Scale factor

When you dilate an object by a scale factor, you multiply its line lengths by the same number.

If EF/AB = 13/7, the scale factor is 13/7.

B. Length of EF

`\begin{array}{rcl}(EF)/(AB) & = & (13)/(7)\\\\(EF)/((17)/(26)) & = & (13)/(7)\\\\EF & = & (13)/(7)*(17)/(26)\\\\ & = &(1)/(7)*(17)/(2)\\\\ & = & \mathbf{(17)/(14)}\\\end{array}\\\text{The length of EF is $\large \boxed{\mathbf{ (17)/(14)}}$}`

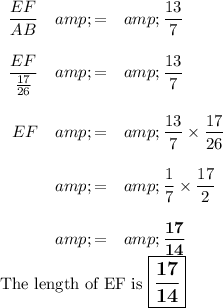
C. Area of EFGH

If the lengths in a shape are all multiplied by a scale factor, then the areas will be multiplied by the scale factor squared.

ABCD is dilated by a scale factor of 13/7, so its area is dilated by a scale factor of

`\left((13)/(7) \right)^(2) = (169)/(49)`

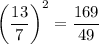
The area of its dilated image EFGH is

`\text{Area of EFGH} = \text{147 in}^(2) * \frac{\text{169}}{\text{49}} = 3 * 169\text{ in}^(2) = 507 \text{ in}^(2)\\\\\text{The area of EFGH is $\large \boxed{\textbf{507 in}^{\mathbf{2}}}$}`