Question

A square tabletop has an area of

(9x2 - 90x+225) cm². The dimensions
of the tabletop have the form cx - di
where cand d are whole numbers. Write
an expression for the perimeter of the
tabletop. Then find the perimeter when
x= 25 centimeters.

Answer 1

s = 3x - 15 is the required expression for perimeter of table top

Perimeter of square tabletop is 240 cm

Solution:

A square tabletop has an area given as:

`(9x^2 - 90x+225) cm^2`

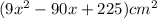
The dimensions of the tabletop have the form cx - di ,where cand d are whole numbers

To find perimeter of tabletop when x = 25 centimeters

Let us first find the length of each side of square

Given area is:

`area = (9x^2 - 90x+225)`

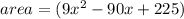
We know that,

`area = (side)^2 = s^2`

Therefore,

`s^2 = (9x^2 - 90x+225)\\\\s^2 = (3x - 15)(3x - 15)\\\\s^2 = (3x - 15)^2`

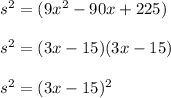
Taking square root on both sides,

s = 3x - 15

The above expression is the required expression for perimeter of table top

To find perimeter when x = 25 centimeter

The perimeter of square is given as:

`perimeter = 4s`

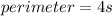
perimeter = 4(3x - 15)

Substitute x = 25

perimeter = 4(3(25) - 15)

perimeter = 4(60) = 240

Therefore perimeter of square tabletop is 240 cm