Question

A student uses pens whose lifetime is an exponential random variable with mean 1 week. Use the central limit theorem to determine the minimum number of pens he should buy at the beginning of a 15-week semester, so that with probability .99 he does not run out of pens during the semester.

Answer 1

Student needs pens= n = 27.04

Rounding off with upper floor function ⇒ n =28

Rounding off with lower floor function ⇒ n =27

Explanation:

Given that lifetime of each pen is a exponential random variable with mean 1 week.

Let
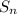`S_(n)` be total sum of lifetime of n pens.

So mean of
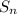`S_(n)` = μ = n.1

Standard deviation of
`S_(n)` =
`\sigma=√(n)`

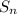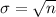
Probability that he doesnot run out of pens= 0.99

Considering Sn be sum of n lifetimes, using central limit theorem

`(S_(n)-n)/(√(n))\approx N(0,1)\\\\P(S_(n)>15)=[P((S_(n)-n)/(√(n)))>(15-n)/(√(n))]\\ 1-\phi((15-n)/(√(n)))=\phi(-((15-n)/(√(n))))=0.99\\`

From table of standard normal distribution

`(15-n)/(√(n))=-2.3263\\15-n=-2.3263√(n)\\n-2.3263-15√(n)`

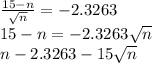
Solving the quadratic Equation in variable x we get

n=27.04