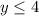Answer:
see the explanation
Explanation:
Verify the range of each quadratic function
case 1) we have
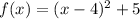
This is a vertical parabola open upward (the leading coefficient is positive)
The function is written in vertex form
The vertex represent a minimum
The vertex is the point (4,5)
The range is the interval [5,∞)
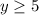
case 2) we have
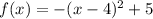
This is a vertical parabola open downward (the leading coefficient is negative)
The function is written in vertex form
The vertex represent a maximum
The vertex is the point (4,5)
The range is the interval (-∞,5]
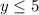
case 3) we have
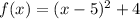
This is a vertical parabola open upward (the leading coefficient is positive)
The function is written in vertex form
The vertex represent a minimum
The vertex is the point (5,4)
The range is the interval [4,∞)
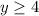
case 4) we have
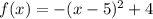
This is a vertical parabola open downward (the leading coefficient is negative)
The function is written in vertex form
The vertex represent a maximum
The vertex is the point (5,4)
The range is the interval (-∞,4]