Question

√−100 = ___ +_____i
...

Answer 1

The square root of -100 is 0 + 10i or simply 10i in the form of a complex number, representing the imaginary part along the complex plane's imaginary axis.

Step-by-step explanation:

The square root of a negative number is not a real number, but rather a complex number denoted by the imaginary unit i for the square root of -1. To find the square root of -100, express -100 as the product of its prime factors:
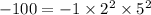`\(-100 = -1 * 2^2 * 5^2\)`. Then, applying the properties of square roots, break it down:
`\(√(-1) * √(2^2) * √(5^2)\)`.

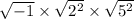The square root of -1 is represented as i, while the square roots of
`\(2^2\)` and
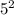`\(5^2\)` are 2 and 5, respectively. Combining these results, the square root of -100 is 0 + 10i, or simply 10i in complex number form, indicating that it lies on the imaginary axis of the complex plane.

It's important to note that the square root of a negative number results in a complex number with a real part of 0 and an imaginary part that represents the square root of the positive value of the number. In this case, the square root of -100 yields an imaginary component of 10i, indicating the distance from 0 along the imaginary axis in the complex plane, demonstrating the nature of complex numbers when dealing with square roots of negative values.