Question

The graphs of y=x-3 and y = 3x -4 intersect at

approximately
1) (0.38,-2.85), only
| 2) (2.62,3.85), only
3) (0.38,-2.85) and (2.62,3.85)
4) (0.38, -2.85) and (3.85,2.62)​

Answer 1

Option 3) (0.38,-2.85) and (2.62,3.85)

Explanation:

The correct question is

The graphs of y=x^2-3 and y=3x-4 intersect at approximately...

we have

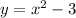`y=x^2-3` ----> equation A

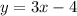`y=3x-4` ----> equation B

Solve the system by graphing

Remember that the solution of the system is the intersection point both graphs

Equate equation A and equation B

`x^2-3=3x-4`

`x^2-3x-3+4=0`

`x^2-3x+1=0`

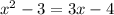
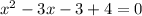
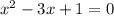
The formula to solve a quadratic equation of the form

`ax^(2) +bx+c=0`

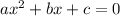
is equal to

`x=\frac{-b\pm\sqrt{b^(2)-4ac}} {2a}`

in this problem we have

`x^2-3x+1=0`

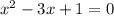
so

`a=1\\b=-3\\c=1`

substitute in the formula

`x=\frac{-(-3)\pm\sqrt{-3^(2)-4(1)(1)}} {2(1)}`

`x=\frac{3\pm√(5)} {2}`

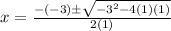
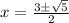
so

`x_1=\frac{3+√(5)} {2}=2.62`

`x_2=\frac{3-√(5)} {2}=0.38`

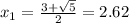
Find the values of y (substitute the value of x in equation A or equation B)

For x=2.62 ---->
`y=(2.62)^2-3=3.85`

For x=0.38 ---->
`y=(0.38)^2-3=-2.85`

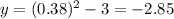
therefore

The intersection points are approximately (0.38,-2.85) and (2.62,3.85)