hmmmm let's say our numbers are "a" and "b", but we know they're consecutive integer, therefore "b" is either a-1 or a+1, hmm let's use the latter
a = first integer
a+1 = second integer
we know their reciprocals add up to 5/6, so
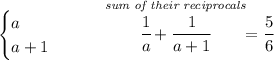
let's use the LCD of (a)(a+1)(6) and multiply both sides by it, to do away with the denominators
![6a(a+1)\left[ \cfrac{1}{a}+\cfrac{1}{a+1} \right]=6a(a+1)\left[ \cfrac{5}{6} \right] \\\\\\ 6(a+1)+6a = 5a(a+1)\implies 6a+6+6a=5a^2+5a \\\\\\ 12a+6=5a^2+5a\implies 0 = 5a^2-7a-6\implies 0 = (a-2)(5a+3) \\\\\\ \begin{cases} 2=a&\textit{\large \checkmark}\\ -(3)/(5)=a&\textit{not an integer} \end{cases}~\hfill \begin{cases} a &= 2\\ a+1 &= 3 \end{cases}](https://img.qammunity.org/2022/formulas/mathematics/college/1mx8vu2k98ukvchlvxwwttf3ar3v6urx6z.png)