Question

Solve the quadratic equation

Answer 1

Our problem is
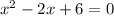`x^2-2x+6=0`, but as we can see, we are unable to factor. We have to use the quadratic equation to solve.

`x^2-2x+6=0`

`(-b+-√(b^2-4ac))/(2a)`

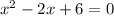
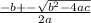
Positive Quadratic Formula:

`(-(-2)+√((-2)^2-4(1)(6)))/(2(1))`

`=(2+√(4-24))/(2)\\=1+(√(-20))/(2)`

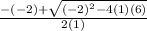
Negative Quadratic Formula:

`(-(-2)-√((-2)^2-4(1)(6)))/(2(1))`

`=(2-√(4-24))/(2)\\=1-(√(-20))/(2)`

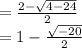
Since both of our answers are the square root of a negative number, we know that the quadratic equation has no real solution.

*We could have also used the Discriminant Test to determine whether the quadratic equation has real roots or not. However, for our means, the quadratic equation seems enough.

Answer 2

D. No real Solution

Explanation:

Hello!

Let's use the quadratic formula:
`x = (-b \pm √(b^2 - 4ac))/(2a)`

In our equation:

• a = 1
• b = -2
• c = 6

This comes from the standard form of a quadratic:
`ax^2 + bx + c`

Now, solve:

• 
  `x = (-b \pm √(b^2 - 4ac))/(2a)`
• 
  `x = (-(-2) \pm √((-2)^2 - 4(1)(6)))/(2(1))`
• 
  `x = (2 \pm √(4 -24))/(2)`
• 
  `x = (2 \pm√(-20))/(2)`
• 
  `x = (2 \pm 2√(-5))/(2)`
• 
  `x = 1 \pm \sqrt{-5`

Since the radicand (-5) is negative, there are no real solutions. The correct answer is Option D.