Solve the equation- (5)/(x - 3) - (4)/(x + 4) = (1)/(x) ​

Question

Solve the equation-

`(5)/(x - 3) - (4)/(x + 4) = (1)/(x)`
​

Answer 1

Hello studentUnion!

`\huge \boxed{\mathfrak{Question} \downarrow}`

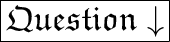
Solve the equation-

`(5)/(x - 3) - (4)/(x + 4) = (1)/(x) \\`

`\large \boxed{\mathfrak{Answer \: with \: Explanation} \downarrow}`

`(5)/(x - 3) - (4)/(x + 4) = (1)/(x) \\`

Let's multiply both the sides of the equation by x (x - 3) & (x + 4) which is the LCM of (x - 3), (x + 4) & x. We can't solve it directly without taking the LCM first as the denominators are not equal to each other. Then do cross multiplication. After all these steps, you'll get an equation as..

`x\left(x+4\right)* 5-x\left(x-3\right)* 4=\left(x-3\right)\left(x+4\right) \\`

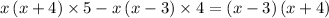
Now, use the distributive property & simplify it.

`x\left(x+4\right)* 5-x\left(x-3\right)* 4=\left(x-3\right)\left(x+4\right) \\ \left(x^(2)+4x\right)* 5-x\left(x-3\right)* 4=\left(x-3\right)\left(x+4\right) \\ 5x^(2)+20x-x\left(x-3\right)* 4=\left(x-3\right)\left(x+4\right) \\ 5x^(2)+20x-\left(x^(2)-3x\right)* 4=\left(x-3\right)\left(x+4\right) \\ 5x^(2)+20x-\left(4x^(2)-12x\right)=\left(x-3\right)\left(x+4\right) \\ 5x^(2)+20x-4x^(2)+12x=\left(x-3\right)\left(x+4\right) \\ x^(2)+20x+12x=\left(x-3\right)\left(x+4\right) \\ x^(2)+32x=\left(x-3\right)\left(x+4\right) \\ x^(2)+32x=x^(2)+x-12 \\ x^(2)+32x-x^(2)=x-12 \\ 32x=x-12 \\ 32x-x=-12 \\ 31x=-12 \\ \boxed{ \boxed{ \bf \: x=-(12)/(31) }}`

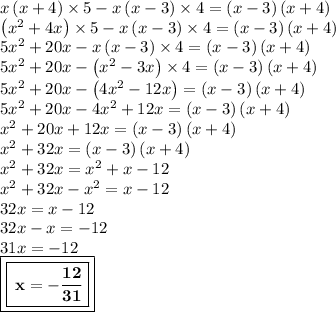
• The value of x is -12/31.

__________________

Hope it'll help you!

ℓu¢αzz ッ

Answer 2

`(5)/(x-3) -(4)/(x+4) =(1)/(x)`

`(5(x+4)-4(x-3))/((x-3)(x+4)) =(1)/(x) \\`

`(5x+20-4x+12)/((x-3)(x+4)) =(1)/(x)`

`(x+32)/((x-3)(x+4)) =(1)/(x)`

Use Cross multiplication

`x(x+32)=(x-3)(x+4)`

`x^(2) +32x = x^(2) +4x-3x-12`

`x^(2) +32x=x^(2) +x-12`

`x^(2) +32x-x^(2) -x=-12`

`31x = -12`

`(31x)/(31) =(-12)/(31) \\x = (-12)/(31)`

Hope this helps you.

Let me know if you have any other questions :-)