Question

Without solving, classify the following system. EXPLAIN your answer in complete sentences.

The equations are y = (2/3)w-1 and -2w+3y=-3

Answer 1

Dependent (consistent) system

Explanation:

The given systems of linear equations, y = ⅔w - 1, and -2w + 3y = -3 are identical.

y = ⅔w - 1

The slope-intercept form of -2w + 3y = -3 is y = ⅔w - 1. In order to prove this statement, transform -2w + 3y = -3 into its slope-intercept form, y = mx + b.

To isolate y, add 2w to both sides:

-2w + 2w + 3y = 2w - 3

3y = 2w - 3

Divide both sides by 3:

`(3y)/(3) = (2w - 1)/(3)`

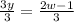
y = ⅔w - 1 ⇒ This proves that both equations in the given system are identical.

If graphed, their lines will coincide and appear as if there is only one line. This characterizes a dependent (consistent) system with infinitely many solutions.

A dependent system has at least one solution; a dependent system is consistent if both equations in the system have the same slope and y-intercepts. They will also have infinitely many solutions because all of the possible solutions are along the same line.

Note:

The transformation of -2w + 3y = -3 into slope-intercept form does not constitute "solving" because the solutions to the given system were not provided in this post.