Consider the equation as shown: (x-a)(y-b) = (x-2a)(y- b/2) x(x + 1/2b) + y(y + a/2) -2xy = 5+(x-y)² On comparing the coefficient, a student says these pairs of equations is con…

Question

asked Jan 5, 2022 16.3k views

1 Answer

TheLifeOfSteve · Answer 1 · 2022-01-12T04:24:57+0000

$\large\underline{\sf{Solution-}}$

First equation is

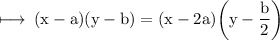
$\rm \longmapsto\:(x - a)(y - b) = (x - 2a)\bigg(y -(b)/(2)\bigg)$

can be further simplified to

$\rm \longmapsto\:xy - bx - ay + ab = xy - (bx)/(2) - 2ay + ab$

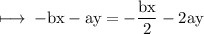
$\rm \longmapsto\: - bx - ay = - (bx)/(2) - 2ay$

$\rm \longmapsto\: - bx + (bx)/(2) = - 2ay + ay$

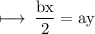
$\rm \longmapsto\: - (bx)/(2) = - ay$

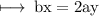
$\rm \longmapsto\: (bx)/(2) = ay$

$\rm \longmapsto\:bx = 2ay$

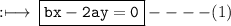
$\rm:\longmapsto \:\boxed{\tt{ bx - 2ay = 0}} - - - - (1)$

Second equation is

$\rm \longmapsto\:x\bigg(x + (1)/(2b) \bigg) + y \bigg(y + (a)/(2)\bigg) - 2xy = 5 + {(x - y)}^(2)$

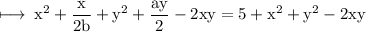
$\rm \longmapsto\: {x}^(2) + (x)/(2b) + {y}^(2) + (ay)/(2) - 2xy = 5 + {x}^(2) + {y}^(2) - 2xy$

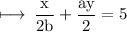
$\rm \longmapsto\: (x)/(2b) + (ay)/(2) = 5$

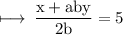
$\rm \longmapsto\: (x + aby)/(2b) = 5$

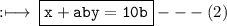
$\rm :\longmapsto\:\boxed{\tt{ x + aby = 10b}} - - - (2)$

So, we have two equations in simplest form as

$\rm \longmapsto\:bx - 2ay = 0$

and

$\rm \longmapsto\:x + aby = 10b$

Now, Consider

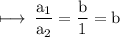
$\rm \longmapsto\:(a_1)/(a_2) = (b)/(1) = b$

$\rm \longmapsto\:(b_1)/(b_2) = ( - 2a)/(ab) = - (2)/(b)$

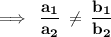
$\bf\implies \:(a_1)/(a_2) \: \\e \: (b_1)/(b_2)$

This implies, System of equations is consistent having unique solution.

So, The student is correct as lines are intersecting.

So, option (b) is correct.