Question

Rationalise the denominator of: 1÷√5+√2​

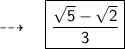
Answer 1

`\boxed{\sf{ (√(5) - √(2) )/(3) }} \\`

Explanation:

`\sf (1)/(√(5) + √(2))`

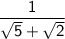
Rationalising the denominator means making the denominator rational. In order to rationalise the denominator, we multiply the rationalising factor of the denominator with both the numerator and the denominator. Rationalising factor is nothing but the terms which is when multiplied with another term, then the another terms becomes rational.

Here, the denominator is in the form of (a + b). The rationalising factor of (a + b) is (a ― b). Henceforth, the rationalising factor of (√5 + √2) will be (√5 ― √2). Now, just multiply (√5 ― √2) with both the numerator and the denominator to rationalise the denominator.

`\dashrightarrow \quad \sf{ (1)/(√(5) +√(2)) * (√(5) - √(2) )/(√(5) - √(2)) } \\`

Rearrange the terms in order to perform multiplication.

`\dashrightarrow \quad \sf{ (1(√(5) - √(2) ) )/((√(5) + √(2))(√(5) - √(2))) } \\`

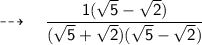
Now, in the numerator we'll perform multiplication using the property of multiplication over addition. And, in the denominator we'll use the identity (a + b)(a — b) = a² — b².

`\dashrightarrow \quad \sf{ (√(5) - √(2) )/((√(5))^2 - √(2)^2) } \\`

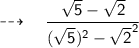
Writing the squares of the numbers in the denominator.

`\dashrightarrow \quad \sf{ (√(5) - √(2) )/(5 -2) } \\`

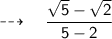
The last step, performing subtraction in the denominator and we'll get the required answer!

`\dashrightarrow \quad \boxed{\sf{ (√(5) - √(2) )/(3) }} \\`